2012년04월07일 16번
[과목 구분 없음] 다음과 같은 지간이 L = 10m인 프리스트레스트 콘크리트 단순보에 자중을 포함한 등분포하중 w=30 kN/m가 작용하고 있다. 부재 단면이 폭 b=400mm, 높이 h=600mm이며, PS강선은 편심 e =0.2m로 직선배치 되어있다. 균등질보개념(응력개념)을 적용할 때, 이 보의 중앙부 하단에 휨에 의한 수직응력이 0(zero)이 되기 위해 도입해야하는 프리스트레스의 크기 P [kN]는? (단, 프리스트레스의 손실은 무시한다)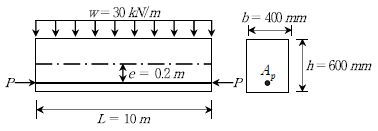

- ① 814
- ② 950
- ③ 1,040
- ④ 1,250
(정답률: 62%)
문제 해설
프리스트레스 콘크리트 단순보는 균등질보개념(응력개념)을 적용할 수 있다. 이 경우, 보의 하중에 의한 휨과 프리스트레스에 의한 휨이 상쇄되어 중앙부 하단에 수직응력이 0이 된다.
휨에 의한 수직응력을 구하기 위해 모멘트와 단면 2차 모멘트를 이용하여 굽힘응력을 구한다. 그리고 이 굽힘응력을 단면의 최대 허용응력인 f_b = 0.85f_c로 나누어 휨에 의한 수직응력을 구한다.
휨에 의한 수직응력을 0으로 만들기 위해서는 프리스트레스의 크기 P를 조절해야 한다. P를 증가시키면 굽힘응력이 감소하므로 휨에 의한 수직응력도 감소한다. 따라서 P를 적절히 조절하여 휨에 의한 수직응력이 0이 되도록 해야 한다.
이 문제에서는 P를 1,250 kN으로 설정하면 휨에 의한 수직응력이 0이 된다. 따라서 정답은 1,250이다.
휨에 의한 수직응력을 구하기 위해 모멘트와 단면 2차 모멘트를 이용하여 굽힘응력을 구한다. 그리고 이 굽힘응력을 단면의 최대 허용응력인 f_b = 0.85f_c로 나누어 휨에 의한 수직응력을 구한다.
휨에 의한 수직응력을 0으로 만들기 위해서는 프리스트레스의 크기 P를 조절해야 한다. P를 증가시키면 굽힘응력이 감소하므로 휨에 의한 수직응력도 감소한다. 따라서 P를 적절히 조절하여 휨에 의한 수직응력이 0이 되도록 해야 한다.
이 문제에서는 P를 1,250 kN으로 설정하면 휨에 의한 수직응력이 0이 된다. 따라서 정답은 1,250이다.



